はじめに

こんにちは、マイクロアドで機械学習エンジニアをしている大庭です。現在はUNIVERSE Adsというプロダクトで入札アルゴリズムの研究開発および実装を担当させていただいてます。今回の記事では、Real-Time-Biddingにおけるオークションの落札額、自社の落札確率を求めるタスクである落札予測に対しLabel Distribution Learning(LDL)という手法を試してみたのでその結果をご紹介したいと思います。

落札予測

落札予測とはRTBのリクエスト情報からそのリクエストがいくらで、どのくらいの確率で落札されるのかを予測するタスクのことです。

落札予測ではモデルの出力が確率分布であることが特徴で、これにより予測結果を「落札額の推定」や「ある入札額で入札した場合の落札確率」など複数の用途に利用できます。

f:id:oba_atsushi:20210720093427p:plain

落札予測の問題設定やモデルの詳細については以下の記事にまとめてあるので、是非こちらの記事もご一読いただければと思います。 developers.microad.co.jp

落札額の離散化

マイクロアドでは落札予測にDeepHit [Lee et al., 2018]モデルを利用しています。このモデルのメリットとして多クラス分類と同じ構造のニューラルネットを利用できモデルの表現力が高いことがあります。

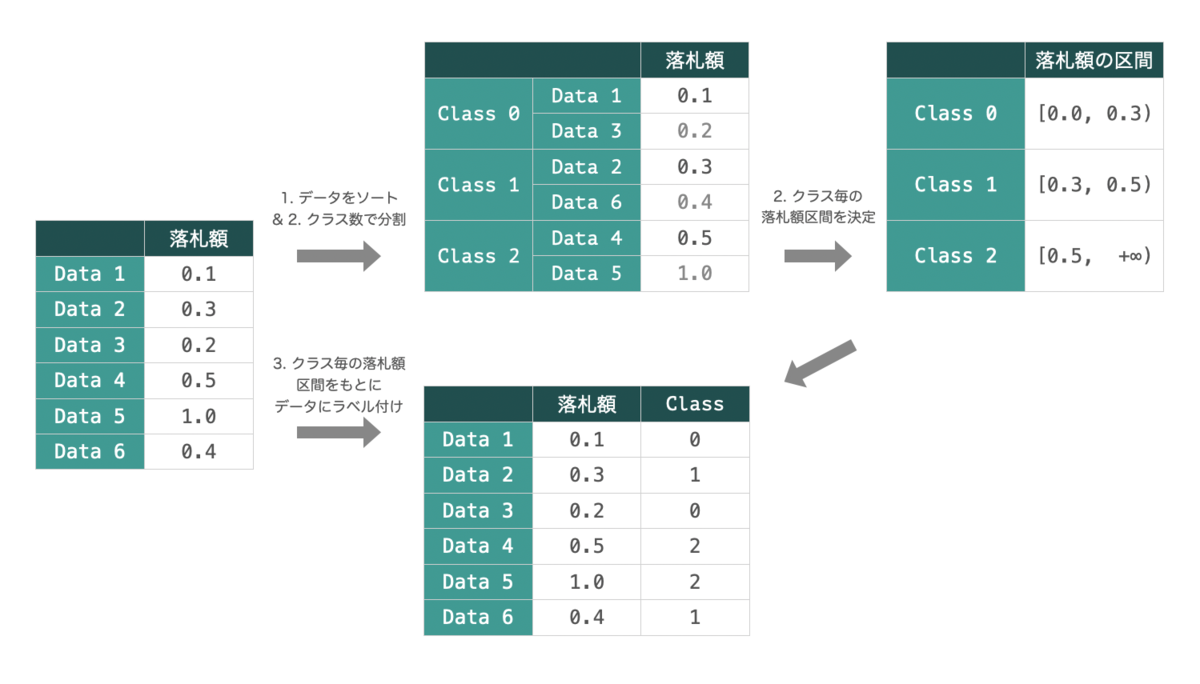
しかし、DeepHitは元々出力が離散のマルチクラス分類の手法であるため、連続的な値である落札額の予測にそのまま適用することはできません。そこで以下のような手順でビニングを行い落札額の離散化を前処理として行っています。

データを落札額でソート
クラス数で分割
クラス毎の落札額区間を決定（Class 0の最小値は $0$ 、Class maxの上限は $+\infty$ で固定）
落札額区間をもとにデータをラベル付け

f:id:oba_atsushi:20210726164231p:plain

離散化の問題点

DeepHitモデルによる損失計算には一般的な多クラス分類問題に用いられるlog lossが利用されています。

$- \sum _ {c = 1}^{M} y_c log(p_c)$

このとき $M$ はクラス数であり、 $y$ はone-hotエンコーディングしたクラスラベル、 $p$ はモデルによる予測確率分布です。

log lossでは損失として考慮されるのは $y_c = 1$ となる正解クラスに対応する $p_c$ のみであり、クラス間の連続性は一切考慮されないという課題が残ります。

そこでLabel Distribution Learning [Xin et al. 2013, Gao et al. 2017]と呼ばれるクラス間に連続性のある多クラス分類問題に用いられる手法を落札予測にも適用することで、この課題の解決を目指しました。

Label Distribution Learning

一般的に多クラス分類問題ではモデルの予測結果である多クラスの確率分布を正解クラスが１、不正解クラスが０であるone-hotベクトルを比較することで誤差の計算を行います。

f:id:oba_atsushi:20210719143153p:plain:w500 — 正解クラスをone-hotに変換した場合の予測確率分布との比較

一方でクラス間に順序があり、あるクラス $n$ が正解の場合その周辺クラスである $n-2$ 、 $n-1$ 、 $n+1$ 、 $n+2$ なども予測として妥当と考えられるようなタスクの場合、周辺クラスも考慮して誤差が計算されるのが望ましいです。

そこでLabel Distribution Learningでは正解クラスを中心とした正規分布に変換した上で誤差の計算を行います。

f:id:oba_atsushi:20210719145001p:plain:w500 — Label Distribution Learningで正解クラスを正規分布に変換した場合の予測確率分布との比較

上図のように正規分布をもとに学習を行うため、正解クラスの周辺も考慮して誤差を求められるような手法となってます。

実装

以下がPytorchでのLabel Distribution Learningの実装になります。正規分布に変換した後のロスの計算についてはCross Entropyを利用しています。

class LDLLoss(nn.Module):
    """
    Label Distribution Learning Loss
    """

    def __init__(self, dist_size, delta: float = 1e-6):
        """
        損失関数の初期設定

        Args:
            dist_size (int): 確率分布のサイズ
            delta (float): log(0)を防ぐための微少数
        """
        super(LDLLoss, self).__init__()
        self.dist_size = dist_size
        self.delta = delta

    def forward(self, P, y) -> torch.tensor:
        """
        損失の計算

        Args:
            P (torch.tensor(batch_size, self.dist_size)): 予測確率分布
            y (torch.tensor(batch_size)): 正解ラベル
        """
        # 正解クラス y を y を中心とした正規分布 Y に変換
        Y = self.norm_dist(y)
        # Cross Entropy
        loss = -Y * torch.log(P + self.delta)
        
        return torch.mean(loss)

    def norm_dist(self, y: torch.tensor, sigma: float = 1.0) -> torch.tensor:
        """
        正解ラベルを正規分布に変換する処理

        Args:
            y (torch.tensor(batch_size)): 正規分布の平均
            sigma (float): 正規分布の分散

        Returns:
            torch.tensor(batch_size, self.dist_size): 正規分布
        """
        batch_size = y.size(0)
        X = torch.arange(0, self.dist_size).repeat(batch_size, 1)
        N = torch.exp(-torch.square(X - y.unsqueeze(1)) / (2 * sigma**2))
        d = torch.sqrt(torch.tensor(2 * math.pi * sigma**2))
        
        return N / d

効果検証

予測落札額の誤差比較

まずはじめにLabel Distribution Learningを用いない場合と用いた場合の落札額予測の精度の比較を行いました。

落札額予測の予測結果はクラスラベルですがそれらは順序をもっているので、正解と予測の距離のズレを考慮した評価を行うため平均絶対誤差を評価指標に利用しています。

また、RTBには1st price auctionと2nd price auctionという２種類の落札額決定方式があるためそれぞれにモデルを用意して検証しています。

	1st price auction	2nd price auction
one-hot	45.323219	14.122518
正規分布(LDL)	37.371838	13.789407

1st price auctionと2nd price auctionの両方で誤差が小さくなっており、Label Distribution Learningが予測精度向上につながっていることが確認できます。

予測分布の視覚的比較

次にモデルの出力である確率分布を可視化することでLabel Distribution Learningがモデルの出力にどのような影響を与えるか、また連続性を考慮した確率分布の学習が行われているかの確認を行いました。

以下がLabel Distribution Learningを用いなかった場合と用いた場合の比較サンプルになります。

左列が正解ラベルをone-hotベクトルに変換した場合、右列がLabel Distribution Learningで正解ラベルを正規分布に変換した場合であり、行ごとに異なるサンプルデータからの比較を行っています。また、赤線はモデルの予測確率分布、青三角は正解落札額、緑三角は予測確率分布から求められる推定落札額をそれぞれ示しています。

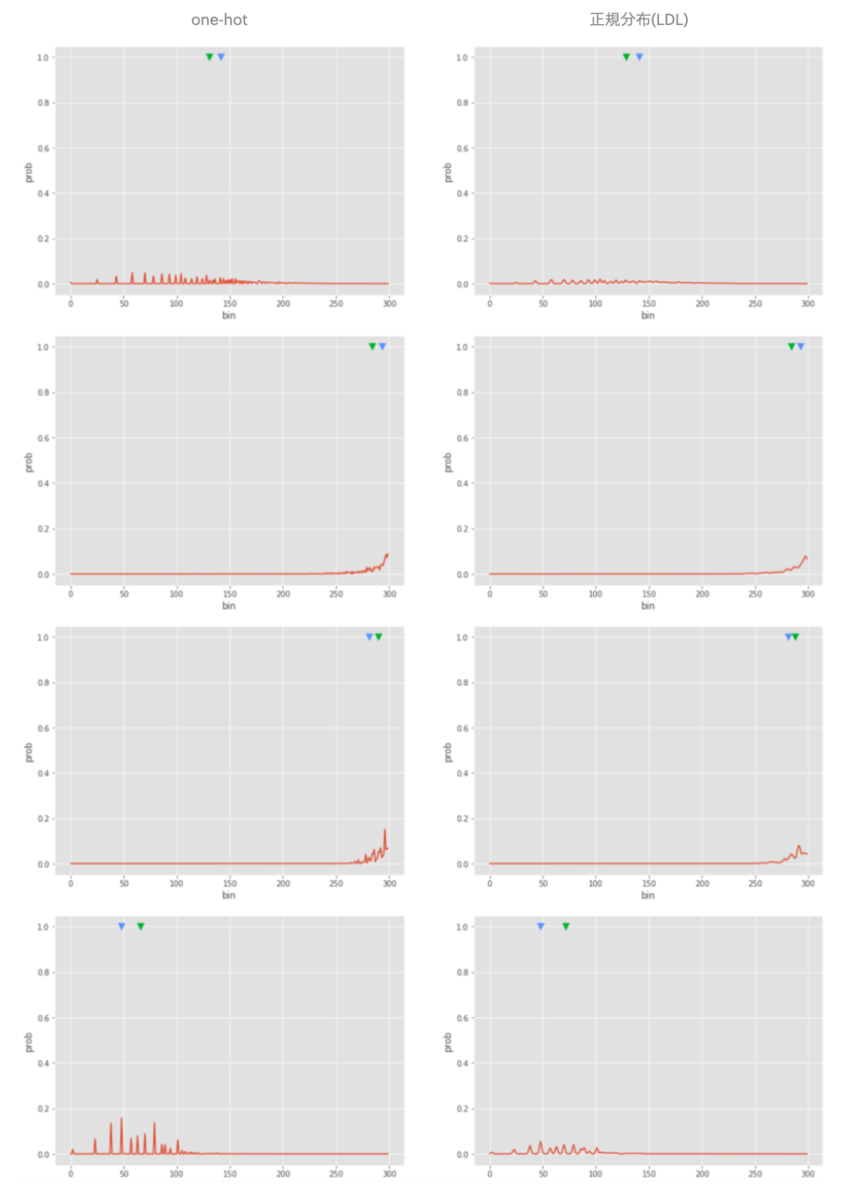
f:id:oba_atsushi:20210730134123p:plain — 予測確率分布の視覚的比較

Label Distribution Learningを用いた場合、予測確率分布がよりなだらかになる効果が確認できました。これはLabel Distribution Learningでは正解クラスを正規分布に変換したものをもとに学習を行うため、正解クラスの周辺も合わせてトレーニングされているためと考えられます。このような傾向からLabel Distribution Learningはクラス間の連続性を考慮して学習が行われていることが確認できます。

おわりに

今回は実際に自社のRTBのログを用いた落札予測に対してLabel Distribution Learningを適用し、効果を確認しました。落札額の予測精度が向上し、また予測分布をよりなだらかにするような効果も見られたため、Label Distribution Learningは落札予測に非常に効果的な手法であると言えそうです。

ここまで記事を読んでくださり、ありがとうございました。