数理最適化による入札関数選択

はじめに

こんにちは. マイクロアドで機械学習エンジニアをしている福島です. 主にReal-Time-Bidding (RTB)におけるClick Through Rate/Conversion Rate(CTR/CVR)予測や入札最適化の研究・開発を担当しています. マイクロアドでは, UNIVERSE Adsというプロダクトで予算消化制御と配信効果の最大化を目的として, 数理最適化による入札関数選択を導入しました.

今回は, 新たに導入した入札最適化について紹介します.

はじめに
問題設定・定式化
試験導入結果
終わりに

問題設定・定式化

RTBでは, 広告主とメディア間でリアルタイムにオークションが開催され, オークションに勝利したDemand Side Platform (DSP)がコストを支払い広告を表示する権利を獲得します.

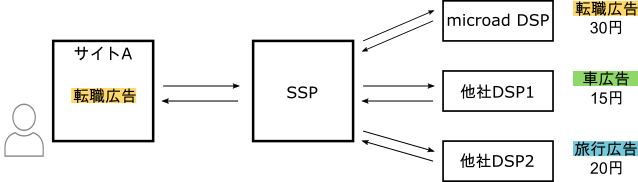
DSPはSupply Side Platform (SSP)からの入札リクエストに対し, 入札対象の広告のCTRやCVR, 落札額などを予測し, それらの情報を用いて入札額を算出します. 入札額を算出する関数(入札関数)の例として, シンプルなものでは以下のようなものがあります.

$\text{入札額} = \text{目標CPC} \times \text{pCTR}$

これは広告キャンペーン¹の目標指標にCPC (Cost Per Click)を利用する場合の例です. ここで, 目標CPCとは広告主が期待するCPCであり, CTR予測による予測CTR(pCTR)との積を入札額として入札することで, 最終的な実績CPCを広告主の目標CPCに合わせることができます.

一方で, 上記の入札関数では予算消化(リーチ数)を担保できません.
予算消化(リーチ数)を重要視する場合, 以下のような入札関数などが考えられます.

$\text{入札額} = \text{予測落札額} + \delta$

ここで, $\delta$ は微小値です. 予測落札額よりもわずかに大きな値で入札することでオークションの勝率を上げることができます.

このように, 入札関数には様々な候補があります. また, 広告キャンペーンごとに予算や目標値などの設定や, CTR/CVRや落札額など市場での振る舞いが大きく異なるため, 全ての広告キャンペーンで同じ入札関数を使うことは適切ではないことが経験的に分かってきました.

そこで, この問題を広告キャンペーンごとに複数ある入札関数の中から最終的な利益を最大にする入札関数の選択問題として考えます.

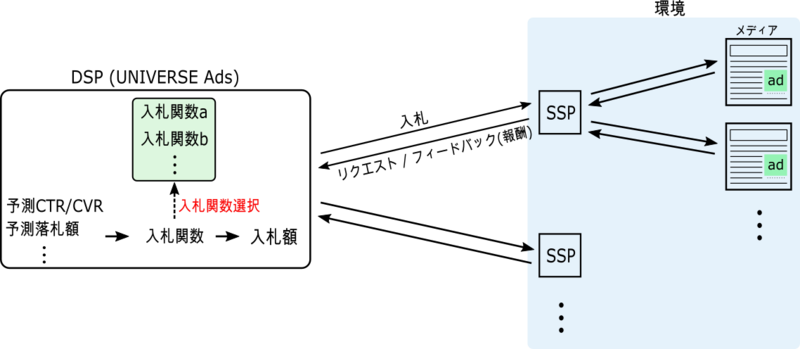
複数ある候補を試しつつ, 最終的な報酬が最大になるように入札関数を選択するという点では, 多腕バンディットに近い問題設定になります. ただし, 予算消化を担保しないといけないため単純なgreedy戦略を取ることはできません.

そこで, 1時間ごとに予算消化を担保しつつ広告効果を最大(配信単価を最小)にする入札関数の適用比率を数理最適化を用いて導出します.

線形計画問題の設計

SSPごとに接続するメディアに差があり, 同じ入札関数でも配信傾向に差があるためSSPごとの適用比率を求めます.
候補となる入札関数集合を $\mathcal{P}$ , DSPが接続するSSP集合を $\mathcal{S}$ として, 以下の線形計画問題を考えます.

$\begin{aligned} &{\rm arg}\min_{\boldsymbol{x}} \sum_{s\in \mathcal{S}} \sum_{p \in \mathcal{P}} {\rm unitprice}_{sp}\cdot x_{sp}\\ \\ &{\rm s.t.} \quad \sum_{s\in \mathcal{S}} \sum_{p \in \mathcal{P}} {\rm cons}_{sp}\cdot x_{sp} \ge {\rm target\_cons} \\ &\quad \quad \sum_{p\in \mathcal{P}}x_{sp} = 1　 (\forall s \in \mathcal{S}) \quad\cdots \text{各制御粒度ごとの合計比率が}1\\ & \quad\quad x_{sp} \ge 0.05 \quad(\forall s \in \mathcal{S}, \forall p \in \mathcal{P}) \quad\cdots \text{最低適用率5%} \end{aligned}$

$x_{sp}$ : SSP $s\in\mathcal{S}$ における入札関数 $p\in\mathcal{P}$ の適用率
${\rm unitprice}_{sp}$ : SSP $s\in\mathcal{S}$ における入札関数 $p\in\mathcal{P}$ の配信単価(CPCなど)
${\rm cons}_{sp}$ : SSP $s\in\mathcal{S}$ における入札関数 $p\in\mathcal{P}$ の期待消化金額²
$\text{target_cons}$ : 次回更新までの目標消化金額

つまり, 広告キャンペーン全体での配信単価(CPCなど)の最小化に対し, 全体での予算消化が目標消化金額以上になる制約を追加しています. また, 適用率が0%になってしまうと, それ以降探索がなくなり情報が全く更新されなくなるため, 非負制約ではなく最低適用率制約を入れています.

予算の分配

毎時間の目標消化金額は, 残り予算 $B$ を推定リクエスト数で分配して算出します.

${\rm target\_cons} = B \cdot \frac{{\rm reqs}(t+1)}{\sum_{i = t+1}^{24} {\rm reqs}(i)}$

期待消化金額の算出

各入札関数の期待消化金額はサンプリングベースで計算します. ただし, 配信設定やユーザーの傾向は変化するため, 直近の情報の影響を大きくする必要があります. そこで, 過去の同じ時間帯の期待消化金額の指数移動平均で計算します.

$\begin{aligned} {\rm cons}_{sp} &= {\rm cons}_{sp} + \alpha(e_{sp} - {\rm cons}_{sp}) \\ e_{sp} &= \frac{g_{sp}}{w_{sp}\cdot p_{sp}} \end{aligned}$

このとき, $g_{sp}$ , $w_{sp}$ , $p_{sp}$ はそれぞれ前日の同じ時間帯の消化金額, 適用率, ペーシング率³です. また, $\alpha$ は減衰率を決めるパラメータです.

※ 保持する情報が少なくて済む計算効率の良い方法でもあります.

試験導入結果

いくつかの広告キャンペーンに適用したところ, 平均で約20%程度Cost Per Action (CPA)の改善を確認できました.

終わりに

今回は, 入札最適化問題を多腕バンディット問題に近い枠組みで考え, 入札関数の最適適用比率の導出を線形計画問題として定式化しました.

機械学習エンジニア絶賛採用中

マイクロアドでは, 問題設定からサーベイ, 開発・運用まで裁量を持ってチャレンジしたいという仲間を募集しています！また, 機械学習エンジニアだけでなく, サーバサイド, フロント, インフラエンジニアなど幅広く募集しています！
気になった方は以下からご応募ください！ recruit.microad.co.jp

広告キャンペーンとは広告を出稿する際の設定上の区分けの概念です. キャンペーンごとに予算や指標などを設定可能です. ads-promo.yahoo.co.jp↩
適用率100%として配信したときに期待される消化金額を期待消化金額と定義しています.↩
ここでのペーシング率はこちらの自動ペーシングによるペーシング率を指しています. developers.microad.co.jp↩