Focal Lossによる自信過剰な予測の抑制

はじめに

こんにちは. マイクロアドで機械学習エンジニアをしている福島です. 主にReal-Time-Bidding (RTB)におけるClick Through Rate/Conversion Rate(CTR/CVR)予測や入札最適化の研究・開発を担当しています. 今回はCTR/CVR予測の学習にFocal Loss [Tsung-Yi Lin et al., 2017]と呼ばれる損失関数を使ってみたのでその結果を紹介したいと思います.

はじめに
Focal Lossとは
CTR/CVR予測にFocal Lossを用いることのモチベーション
- Focal Lossによるcalibrationの改善
検証
まとめ

Focal Lossとは

一般的にCTR/CVR予測は学習データ中でclick/conversionが発生したものを1, そうでないものを0とした教師あり分類問題として扱われます. 正解ラベル $y\in \{1, 0\}$ の2クラス分類問題で一般的に用いられるクロスエントロピー損失関数 $\mathcal{L}_c$ は次のように定義されます.

$\mathcal{L}_c(p, y) = \left\{ \begin{array}{l} - \log(p) \;\;{\rm if} \;\; y = 1\\ - \log(1-p) \;\;\text{otherwise.} \end{array} \right.$

ここで, $p \in [0,1]$ は識別モデルのクラス $y=1$ の予測確率であり,

$p_{{\rm t}} = \left\{ \begin{array}{l} p \;\;{\rm if} \;\; y = 1\\ 1-p \;\;\text{otherwise.} \end{array} \right.$

としたとき, $\mathcal{L}_c$ は次のように書き直すことができます.

$\mathcal{L}_c(p, y) = \mathcal{L}_c(p_{{\rm t}}) = - \log(p_{\rm t})$

Focal Loss $\mathcal{L}_f$ は $\mathcal{L}_c$ を動的にスケーリングしたものであり, 次のように定義されます.

$\mathcal{L}_f(p_{{\rm t}}) = -(1-p_{{\rm t}})^{\gamma}\log(p_{\rm t}), \quad \gamma \ge 0$

$\gamma = 0$ としたとき, $\mathcal{L}_{f}$ と $\mathcal{L}_c$ は一致します. $\gamma$ を変化させた場合, 次の図のようになります.

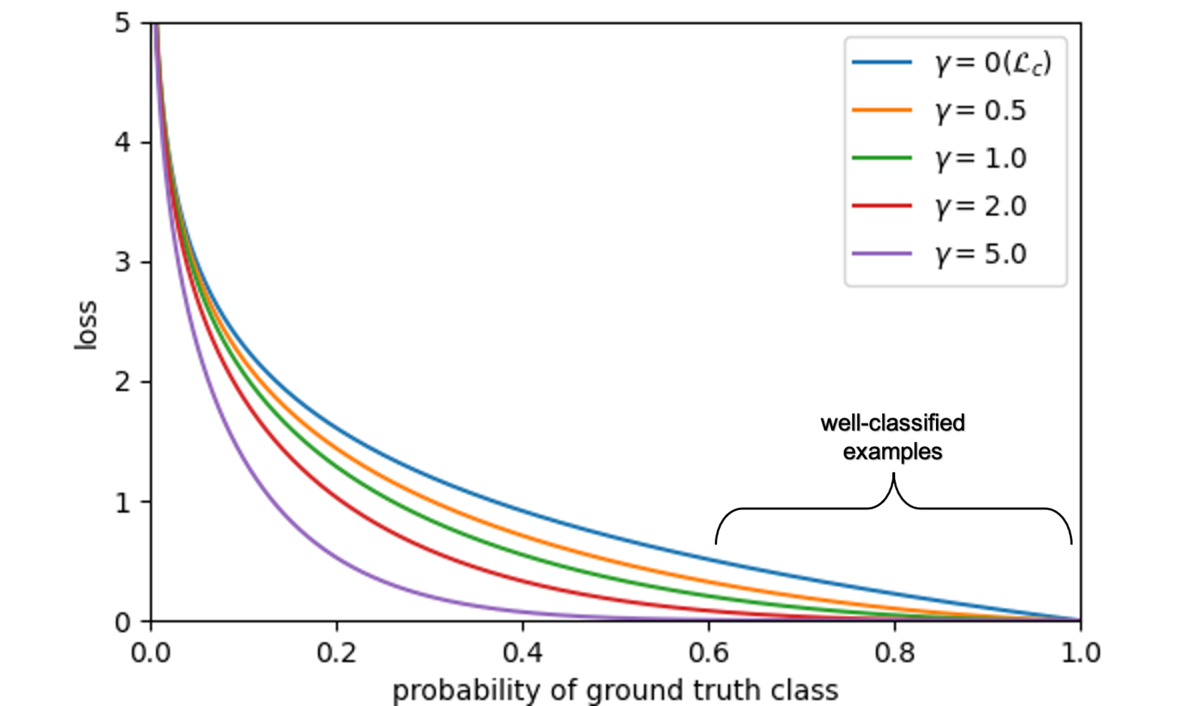
f:id:fukushima-08:20210402165251p:plain — [Tsung-Yi Lin et al., 2017]を参考

上図において, 青線が $\mathcal{L}_c$ です. $\mathcal{L}_c$ では正しく分類されているサンプル(上図のwell-classified examples)に対してもある程度の損失が発生します.

学習データが不均衡(正例数 << 負例数)の場合, 多数クラスの損失を合計すると少数派クラスの損失を圧倒してしまい, 少数派データを無視してしまう可能性があります.

$\mathcal{L}_f$ では, 分類が簡単なeasy exampleに対する損失を小さくし, 分類が難しいhard exampleに対する損失を大きくするように $\mathcal{L}_c$ をスケーリングすることで少数派クラスの損失が潰れることを防いでいます.

CTR/CVR予測にFocal Lossを用いることのモチベーション

CTR/CVR予測の学習データは正例( $y=1$ )に比べ, 負例( $y= 0$ )が圧倒的に多いです. そのため, 正例のデータが過小評価されることが発生し得ると考えました. そこで, hard exampleに対する損失の重みを高くするFocal Lossは有用なのではと考えました.

また, 現在マイクロアドでは2クラス分類モデルにLightGBMを採用しています. *1 Neural Networkや勾配ブースティングのような容量の大きいモデルにおいては, クロスエントロピーに対してモデルがover fitすることで出力が自信過剰になることが経験的に知られています. [Chuan Guo et al., 2017] CTR/CVR予測のような確率推論タスクにおいては, 出力値が実際の確率と近いかどうかであるcalibrationの良し悪しが非常に重要となります. [Gabriel Pereyra et al., 2020]において, Focal Lossを用いることでcalibrationの改善が期待できることがわかっています.

Focal Lossによるcalibrationの改善

ここでは2クラス分類を多クラス分類に一般化して考えます. $y \in \{1, \ldots, K\}$ とし, $p$ と $q$ をそれぞれ予測分布とターゲット分布とします. また, $p_y$ と $q_y$ をそれぞれ $p$ と $q$ のクラス $y$ の成分とします.

ここでFocal Loss $\mathcal{L}_f$ を考えます.

$\mathcal{L}_f = -\sum_{y=1}^K (1- p_y)^{\gamma}q_y \log p_y$

$p_y\in[0,1]$ であるため, ベルヌーイの不等式より,

$\ge -\sum_{y=1}^K (1-\gamma p_y)q_y \log p_y$

$\forall y, \log p_y \le 0$ であるので,

$= -\sum_{y=1}^Kq_y\log p_y - \gamma \left| \sum_{y=1}^K q_y p_y \log p_y\right|$

ヘルダーの不等式より,

$\ge -\sum_{y=1}^Kq_y\log p_y - \gamma \max_{j}q_j \sum_{y=1}^K | p_y \log p_y|$

$\forall j, q_j \in [0,1]$ より,

$\begin{align} &\ge -\sum_{y=1}^Kq_y\log p_y + \gamma \sum_{y=1}^K p_y\log p_y \\\ &= \mathcal{L}_c - \gamma \mathbb{H}[p] \end{align}$

ここで, $\mathbb{H}[p]$ は予測分布 $p$ のエントロピーです. また, $p$ と $q$ のKullback-Leibler divergence ( $\rm KL$ ダイバージェンス)を ${\rm KL}(q||p)$ としたとき $\mathcal{L}_c = {\rm KL}(q || p) + \mathbb{H}[q]$ より,

$\mathcal{L}_f \ge {\rm KL}(q || p) + \mathbb{H}[q] - \gamma \mathbb{H}[p]$

このとき, $\mathbb{H}[q]$ は定数項なので, 次の結果を得ることができます.

$\mathcal{L}_f \ge {\rm KL}(q || p) - \gamma \mathbb{H}[p]$

つまり, Focal Lossを最小化することは, ターゲット分布 $q$ と予測分布 $p$ の ${\rm KL}$ ダイバージェンスの最小化に対して予測分布 $p$ のエントロピーを大きくするような正則化(maximum-entropy regularize [Pereyra, 2017])を行っていると解釈することができます.

予測分布がより高いエントロピーを持つように促すことで, 自信過剰な予測を回避することができ, calibrationが改善することが期待できます.

以上のように, 学習データが非常に不均衡であり, calibrationが重要なタスクであるCTR/CVR予測におけるFocal Lossの効果を確認するために今回の検証を行いました.

検証

ここではCVR予測に用いるLightGBMの目的関数にクロスエントロピー損失とFocal Lossを用いた場合の比較を行います.

LightGBMで自作の目的関数を用いる

LightGBMのTraining APIではfobjパラメータに自作の損失関数を渡すことができます.

fobj (callable or None, optional (default=None)) – Customized objective function. Should accept two parameters: preds, train_data, and return (grad, hess).

引数に予測値と学習データセットを取り, 戻り値に1階微分と2階微分を返す関数を設計する必要があります. 今回Focal Lossを用いるにあたって, 下記のような実装にしました.

def focal_loss(x: np.ndarray, dtrain: lgb.Dataset, gamma: float) -> np.ndarray:
    """損失計算"""
    x = sigmoid(x)
    x[t == 0] = 1 - x[t == 0] 
    retrun  -1 * (1 - x)**gamma * np.log(x)

def focal_loss_grad_hess(x: np.ndarray, dtrain: lgb.Dataset, gamma: float) -> (np.ndarray, np.ndarray,):
    """Focal Lossのgradientとhessianを返す"""
    t = dtrain.label
    grad = derivative(lambda _x: focal_loss(_x, t, gamma=gamma), x, n=1, dx=1e-6)
    hess = derivative(lambda _x: focal_loss(_x, t, gamma=gamma), x, n=2, dx=1e-6)
    return grad, hess


fobj_focal_loss = lambda x,y: focal_loss_grad_hess(x, y, gamma)
model = lgb.train(params, train_set=train_set, fobj=fobj_focal_loss)  # 学習

calibrationの評価指標

calibrationの良し悪しの評価には一般的にexpected calibration error ( $\rm ECE$ ) [Mahdi P. N. et al.]や $\rm ECE$ を拡張した評価指標が用いられます.

予測ラベルを $\hat{y}$ , 予測確率を $p$ としたときの $\rm ECE$ は次のように定義されます.

${\rm ECE} = \mathbb{E}_{p}[|\mathbb{P}(\hat{y}=y|p) - p|]$

つまり, 予測確率と正解率の差の予測確率 $p$ に関する期待値を評価してます.

ただし, $p\in[0,1$ ]は連続値であるため, 一般的には予測確率を $M$ 個のビンに区切って計算します. $i$ 番目のビンに含まれるサンプルの集合を $B_i$ としたとき, $\rm ECE$ は次のように計算されます.

$\begin{align} {\rm ECE} &= \sum_{i=1}^{M} \frac{|B_i|}{N}|A_i -C_i| \\\ A_i &= \frac{1}{|B_i|}\mathbb{1}(\hat{y}=y) \\\ C_i &= \frac{1}{|B_i|}\sum_{j\in B_i} p_j \end{align}$

${\rm ECE}$ はビンが等間隔になっており, サンプル数の多い区間が重要視されてしまうため, 今回は全てのビンに含まれるサンプルサイズが等しくなるようなビンに区切るadaptive ${\rm ECE}$ を用います.

また, CTR/CVR予測は分類タスクではなく確率推論タスクであるため, $y=1$ である確率と予測確率の解離を評価するために, 以下のように定義します.

$\begin{align} A_i &= \frac{1}{|B_i|}\mathbb{1}(y=1) \\\ C_i &= \frac{1}{|B_i|}\sum_{j\in B_i} p_j \end{align}$

実験では, Normalized Entropy, Precision-Recall AUC (PR-AUC)*2の値も確認します.

実験

CVR予測の検証用の小規模なテストデータセット(テストサンプルサイズ: 4818)でFocal Lossの効果を確認します.

最小化する目的関数以外のLightGBMのハイパーパラメータには同じ値を用い, Focal Lossのパラメータである $\gamma$ は予め調整済の値を用いたときの結果は以下の通りです.

目的関数	Normalized Entropy	PR-AUC	adaptive $\rm ECE$
クロスエントロピー	0.81421829	0.015134088	0.001602728
Focal Loss	0.83528439	0.018361536	0.001566031

Focal Lossを用いた場合の方がPR-AUCが高いことから, 少ない正例を正しく識別できるようになっていることがわかります. これは, Focal Lossがhard exampleに対する損失を高くすることで, 少数派の損失を考慮しやすくなっているためだと考えられます. 一方で, Focal Lossを用いた場合の方がNormalized Entropyは高くなっています. モデルの識別能力が同等程度でありデータが不均衡な場合, 出力に対する自信が高いほどNormalized Entropyは低くなりやすいため, Focal Lossを用いることで予測値に対する自信が全体的に下がっていると判断できます. adaptive $\rm ECE$ は同程度であるため, calibrationの性能は同程度であると言えます.

まとめ

今回Focal Lossの検証を行い, Focal Lossが期待通りの挙動をすることが確認できました. 正例の識別能力は上がっており, 予測分布のエントロピーが高くなっているので, データが不均衡かつ予測値が自信過剰である場合は自信過剰な予測を抑制できるため有用であると言えそうです.

一方で, どの程度hard exampleを考慮するかはパラメータ $\gamma$ に依存しており, $\gamma$ の変化による出力値の変化は大きい印象がありました. また, 予測分布のエントロピーが高くなるということは, 負例が圧倒的に多い状況においては予測値の高騰に繋がり易いという側面もあるので, CTR/CVR予測においてFocal Lossが有益であると断言するのは難しいとも感じました.

ですが, モデルの出力を直接ターゲットとしたcalibrationの改善*3は面白い取り組みではあるので引き続き調査していきたいと思いました.

機械学習エンジニア絶賛採用中

マイクロアドでは, 問題設定からサーベイ, 開発・運用まで裁量を持ってチャレンジしたいという仲間を募集しています！また, 機械学習エンジニアだけでなく, サーバサイド, フロント, インフラエンジニアなど幅広く募集しています！
気になった方は以下からご応募ください！ recruit.microad.co.jp

参考文献

Focal Loss for Dense Object Detection, Tsung-Yi Lin et al., ICCV2017

On Calibration of Modern Neural Networks, Chuan Guo et al., ICML2017

Calibrating Deep Neural Networks using Focal Loss, Jishnu Mukhoti et al., NeurIPS2020

Regularizing Neural Networks by Penalizing Confident Output Distributions, Gabriel Pereyra et al., ICLR2017

Obtaining Well Calibrated Probabilities Using Bayesian Binning, Mahdi P. N. et al., AAAI2015

*1:developers.microad.co.jp

*2:PR-AUC: 正例を正しく正例と判断できているかに着目している. データが不均衡(正例数 << 負例数)であるほど値のスケールは小さくなる

*3:現在マイクロアドではモデルの学習とは別にIsotonic Regressionによるprobability calibrationを導入しています.developers.microad.co.jp