CTR予測における確率補正について

はじめに

こんにちは. マイクロアドで機械学習エンジニアをしている福島です. 主に広告のClick Through Rate (CTR)予測やReal-Time-Bidding (RTB)の入札最適化を担当しています. 今回はマイクロアドでのCTR予測における確率補正について紹介したいと思います.

はじめに
CTR予測とは
CTR予測における確率補正
終わりに

CTR予測とは

RTBでは下図のように, 広告主とメディア間でリアルタイムにオークションが開催され, オークションに勝利した広告がメディアに表示されます.

f:id:fukushima-08:20210119170631p:plain

マイクロアドでは現在オークションの入札額は次のように予測CTRと目標CPC(Cost per Click)の積に依存する形で決定しています. Zhang, 2014

$\text{入札額} \propto \text{目標CPC} \times \text{予測CTR}$

CTRは広告が表示されたときにクリックされる確率で, 過去の配信ログから機械学習モデルを学習して予測しています. オークションの勝率・配信効果に直結するため, 正確なCTRを予測することが求められます.

f:id:fukushima-08:20210119152312p:plain

一般的にCTR予測は学習データ中のクリックされたものを1, クリックされなかったものを0として教師あり2クラス分類問題として扱われます. この問題を解くための手法としては, ロジスティック回帰や深層学習ベースの手法, 決定木ベースの手法など様々なものがありますが, CTR予測を2クラス分類問題として考える場合, 次のような3つの問題があります.

問題1　学習データが不均衡

マイクロアドでは1日に100億以上の入札リクエストがあるため, 蓄積されるログもその分膨大になりますが, 平均的なCTRは高くないため, ほとんどが負例(クリックなし)のデータになります. 学習時間の短縮や使用メモリの制限から, 負例のデータを全て用いるのではなく, ランダムにアンダーサンプリングして使用しています. 負例をアンダーサンプリングすることで, 学習データの分布が本来の分布とずれてしまい, 機械学習モデルがCTRを過大に予測してしまうことにつながります.

問題2　機械学習モデルの出力を確率として扱うのは不適切な場合がある

深層学習のような表現力の高いモデルなどは, 予測値が自信過剰になることが経験的に知られており, 2クラス分類の出力値 $y \in [0, 1$ ]をそのまま予測CTRとして扱うのは不適切な場合があります.

問題3　学習データの信頼度が高くない

広告が表示された時にクリックするかどうかはその時の状況にも依存し, 同じ広告が同じユーザーに配信されたとして, 必ずしもクリックされるとは限りませんが, 学習データ上は過去の配信結果から作成されているので学習データにおける正例は必ずクリックされることを仮定してしまっています. そのため, 予測値が実際のCTRと乖離してしまう場合があります.

上記の3つの問題に対して, マイクロアドでは機械学習モデルの出力を以下の2つの方法で補正し, 予測CTRを求めています.

CTR予測における確率補正

アンダーサンプリングによって生じたバイアスの除去

こちら問題1に対する解決策です.

マイクロアドではアンダーサンプリングによって生じたバイアスの除去にAndrea Dal Pozzolo, 2015の手法を用いています. 分類器への入力を $x \in \mathbb{R}^d$ , 出力を $y \in \{0, 1\}$ として, $f: \mathbb{R}^d \rightarrow \{0,1\}$ の2クラス分類問題を考えます. また, 正例が負例に比べ極端に少なく, アンダーサンプリングによるリバランスを行うと仮定します. アンダーサンプリング前の不均衡なデータセットを $(\mathcal{X}, \mathcal{Y})$ とし, アンダーサンプリング後のデータセットを $(X, Y)$ とします. つまり, $(X, Y) \subset (\mathcal{X}, \mathcal{Y})$ です. $(X, Y)$ と $(\mathcal{X}, \mathcal{Y})$ で学習した時の事後確率の変化から, アンダーサンプリングでリバランスした場合の補正式を導出します.

変数 $s$ を $x, y \in (\mathcal{X}, \mathcal{Y})$ に対し $x, y \in (X, Y)$ であれば $s=1$ , $x, y \notin (X, Y)$ であれば $s=0$ としたとき, 変数 $s$ は $x$ に依存しないとすれば次のことが言えます.

$p(s|y, x) = p(s|y)\\ p(x|y, s) = p(x|y)$

つまり, 大多数のクラス(負例)のデータをランダムに削除してもクラス内のデータ分布は変化しません. アンダーサンプリングすることで, クラスの事前確率は変化します.

$p(y|s=1) \neq p(y)$

つまり, クラスの条件付き確率も変化します.

$p(y|x, s=1) \neq p(y|x)$

ベイズの定理より,

$\displaystyle{ p(y|x, s=1) = \frac{p(s=1|y=1)p(y=1|x)}{p(s=1|y=1)p(y=1|x) + p(s=1|y=0)p(y=0|x)} }$

ここで, $(\mathcal{X}, \mathcal{Y})$ の正例を全て含むようにアンダーサンプリングをすれば, $p(s=1|y=1)=1$ であるため,

$\displaystyle{ p(y|x, s=1) = \frac{p(y=1|x)}{p(y=1|x) + p(s=1|y=0)p(y=0|x)} }$

となります. ここで, $\beta = p(s=1|y=0)$ , $p = p(y=1|x)$ , $p_s = p(y|x, s=1)$ とすれば, 次の結果を得ることがでます.

$\displaystyle{ p = \frac{\beta p_s}{\beta p_s - p_s + 1} }$

このとき, $\beta$ は負の事例のアンダーサンプリング率, $p_s$ はアンダーサンプリング後のデータセット上での正のクラスの事後確率です. $p_s$ と $\beta$ からアンダーサンプリングしていない場合のデータセット上での正のクラスの事後確率 $p$ を求めることができます.

Isotonic Regressionによる確率補正

こちら問題2, 問題3に対する解決策です.

学習データの信頼度が低いことへの対処と分類器の出力を妥当な値に補正することを目的としてAlexandru Niculescu-Mizil, 2005によるIsotonic Regressionを用いた確率補正を適用します. 分類器の学習データとは別に確率補正に用いるIsotonic Regressionの学習用のデータセットを準備します. 学習済の分類器を $f(\cdot)$ としたとき, Isotonic Regressionの学習データを $\{(y_i, f_i)\}_{i=1}^N$ とします. このとき, $y_i\in \{0,1\}$ は正解ラベル, $f_i$ は学習した分類器の出力であり, 単調増加な関数 $m(\cdot)$ を学習します.

$y_i = m(f_i) + \epsilon_i$

このとき, 平均二乗誤差を最小化する単調増加な等張関数を学習します.

$\hat{m} = \arg\min_{z} \sum_{i=1}^N (y_i - z(f_i))^2$

この解を求めるアルゴリズムの一つにpair-adjacent violators(PAV) algorithm [Ayer et al., 1955]があります.

f:id:fukushima-08:20210119162555p:plain — [Alexandru Niculescu-Mizil, 2005]から引用

PAV algorithmでは以下の手順で学習しています

確率補正の学習用データセット $\{(y_i, f_i)\}_{i=1}^N$ を $f_i$ の順にソート
$\hat{m}（f_i）=y_i$ で初期化
正解ラベルの順序に間違いがあれば平均値で置換 (分類器が事例を正しくランク付けできているならば, 全ての負例は正例よりも前にくるはず)
推論の際に学習データセット中にない値は, 最近傍の値を出力

つまり, 分類器が事例を正しくランク付けできている部分では少ない事例で平均化し, ランク付けが間違っている部分(分類器の信頼度が低い部分)では, より多くの事例で平均化しています. 確率補正において, Isotonic Regressionは分類器がどれだけ事例を正しくランク付けできるかによって, 境界の位置とビンのサイズが決定されるビニングアルゴリズムとしてみることができます. CTR予測にIsotonic Regressionを用いた場合, 次のような結果になります.

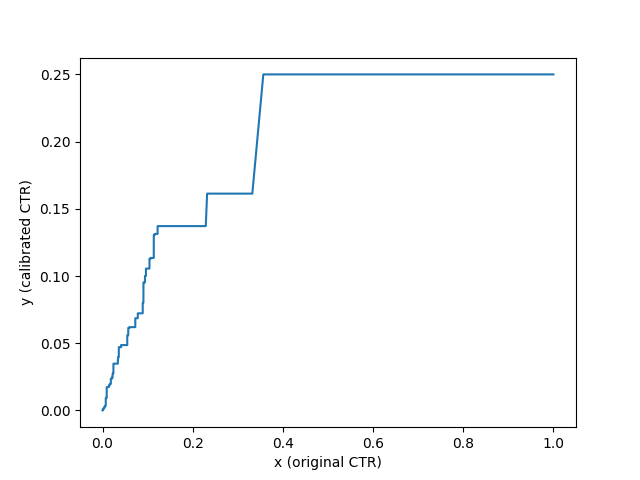
f:id:fukushima-08:20210119223430p:plain — Isotonic Regressionの学習結果の例. x軸: 補正前CTR, y軸: 補正後CTR

確率補正の効果検証

確率補正を行う場合の学習の流れは以下の図のようになっています. マイクロアドでは現在, CTR予測の学習に2週間分の配信ログを用いています. 2週間分の配信ログから負例のアンダーサンプリングを行った学習データを用いて機械学習モデルを学習した後, 学習に用いたデータとは別の未知の補正用データ(次の日の配信ログ)の推論結果を用いてIsotonic Regressionの学習を行っています.

f:id:fukushima-08:20210119191127p:plain — 学習フロー

2021年の1/10〜1/15の配信ログに対して, 上記の確率補正を行ったときのcalibrationとnormalized entropyの推移を以下に示します.

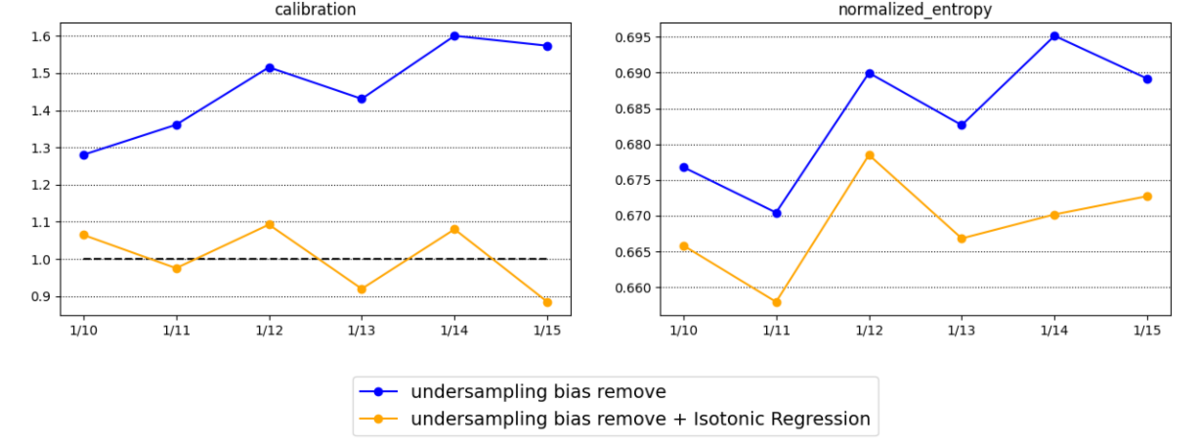
f:id:fukushima-08:20210120143009p:plain — 検証結果. 左: calibration, 右: normalized entropy

$\text{calibration} = \frac{\text{予測CTRの平均値}}{\text{実績CTR}}$

確率補正を行うことで予測CTRの平均値が実績値に近い値になっており, normalized entropyも低くなっています.

※ 2クラス分類にはマイクロアドで現在使っているLightGBMを用いています. developers.microad.co.jp

終わりに

確率予測タスクはシンプルな分類や回帰タスクに比べると複雑ですが, 分類器の精度をあげるのではなく, 適切に出力を補正することでも精度を向上させることができました.

機械学習エンジニア絶賛採用中

マイクロアドでは, 問題設定からサーベイ, 開発・運用まで裁量を持ってチャレンジしたいという仲間を募集しています！また, 機械学習エンジニアだけでなく, サーバサイド, フロント, インフラエンジニアなど幅広く募集しています！
気になった方は以下からご応募ください！ recruit.microad.co.jp

参考文献

Optimal Real-Time Bidding for Display Advertising, Zhang, 2014

Calibrating Probability with Undersampling for Unbalanced Classification, Andrea Dal Pozzolo, 2015

Predicting Good Probabilities With Supervised Learning, Alexandru Niculescu-Mizil, 2005