はじめに
こんにちは、19新卒バックエンドエンジニアの飛田です。
弊社では、プロダクトの一部にCatsという関数型プログラミングを行うためのライブラリを導入しており、今後、Catsをより多くのプロダクトに使用していく予定です。
Catsにはモナドやファンクタという概念が登場しますが、これらの概念は圏論に由来しています。圏論を勉強することで、Catsで登場する諸概念をより深く理解することができると考え、今回、圏論の初歩の内容を自分でまとめてみることにしました。
なお、マイクロアドの優秀なデータサイエンティストであり、数学や物理に大変に詳しいT先輩(アイコンがおふとん)にレビューを依頼することにしました。

レビューをしてもらった結果
まとめた内容の初稿をT先輩にレビューをしていただいたところ、以下の通りものすごい量のツッコミを食らってしまいました。
レビューと修正を繰り返して
というところまでは持っていくことができました。 なお、最初に書いた内容はほとんど生き残りませんでした。
以下がその内容となります。
圏とは
圏とは対象と射の集まりです。ただし、射は結合律と恒等律を満たす必要があります。
対象
対象とは、ありあらゆるモノを抽象化した点のようなもので、それ以上のものではありません。対象を図示すると以下のようになります。

図には、点がいくつかありますが、これらが対象です。
対象の具体例
対象はありとあらゆるモノを抽象化したものなので、具体的な例を当てはめることができます。たとえば、上図の一番左の点は「Jamesという人」です。その隣の点は、「Johnという人」です。さらにその隣の点は、「Robertという人」です。
...と、こんな感じに具体例を当てはめることが可能です。
射
射とは、始点となる対象と終点となる対象をもつ概念で、それ以上のものではありません。 射を図示すると次のようになります。

この図の矢印が射です。射は、始点と終点の対象のみあれば定義できる、抽象的な概念です。具体例を当てはめると、対象は「James」です。対象
は「John」です。
射
は「交友関係」を表しています。これは人間関係を射で表した人間の圏です。
図には、対象間に射が1つしか存在しませんが、対象間に射は複数存在できることに注意してください。
合成
射は合成することができます。
対象と
の間に射
が存在し、
と
の間に
が存在する場合を考えます。

この場合、 必ずと
の合成
が存在します。射
と射
の合成
は一意であることに注意してください。射自体は、無数に存在しえますが、特定の2つの射の合成は1つしか存在しないということです。
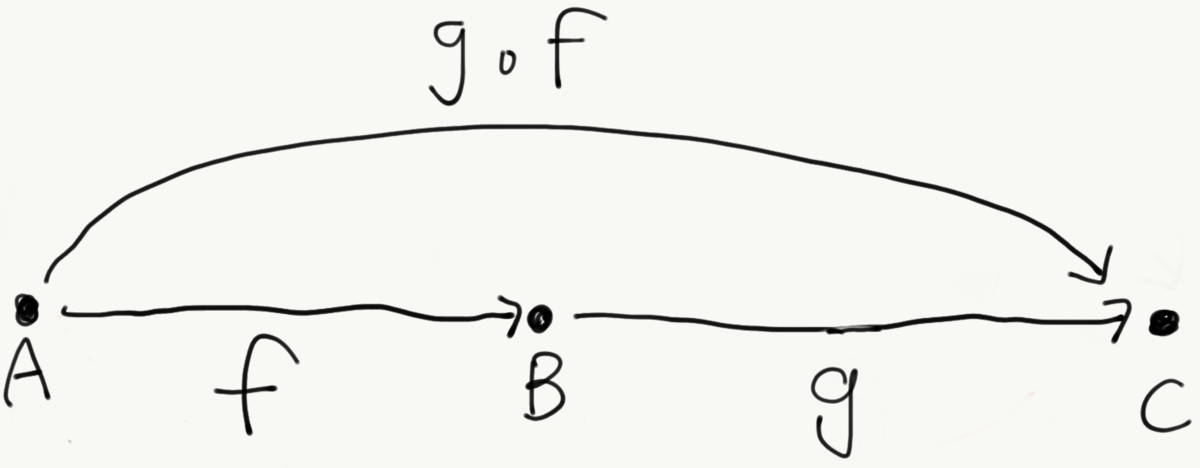
※ の読み方は
g after fです。
結合律
射は結合律と恒等律を満たす必要があります。まず、結合律から説明します。
以下の図を見てください。

このとき、射、
、
は以下の条件を満たします。
図には、 射、
、
とその合成射が存在しますが、合成の順序に関わらず、数式の左辺と右辺が等しくなるということです。これを結合律と言います。
恒等律
すべての対象は恒等射という射を持っています。
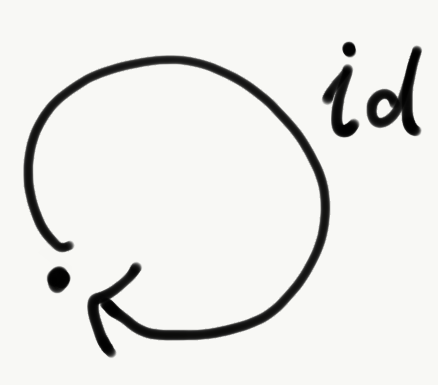
恒等律とは、任意のと
について
と
が成り立つことです。
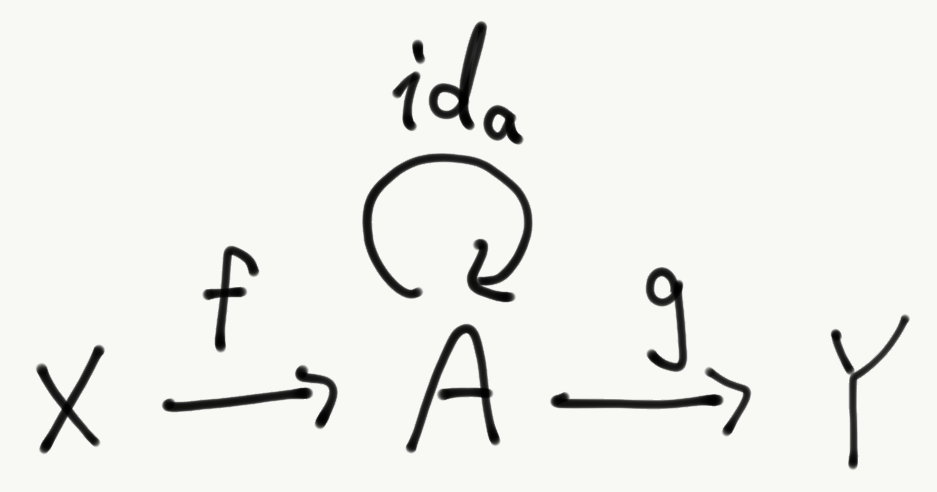
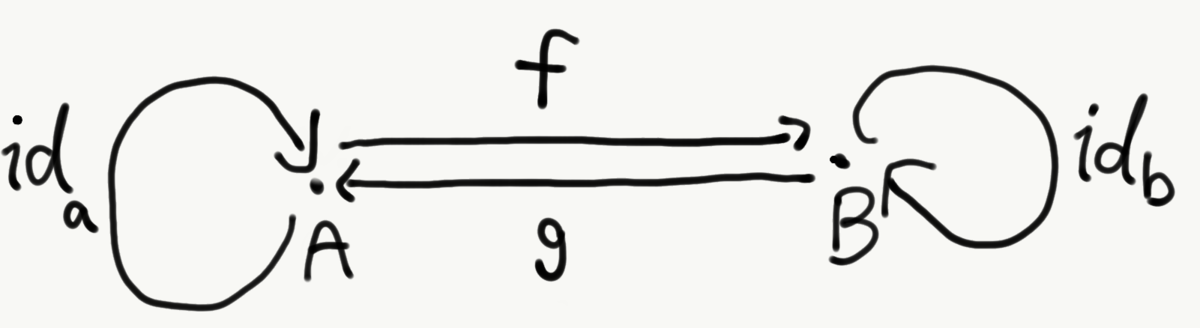
同型
次の図のような射を考えます。このとき、と
が成り立てば、射
と
は同型射と言います。また、対象
と
を結ぶ同型射が存在するとき、
と
は同型と言います。
圏の具体例(前順序の圏)
圏の具体例として、前順序の圏について説明します。
- 前順序圏の対象は集合
の要素
です。
- 射は前順序(
)です。
つまり、前順序の圏とは、不等号を射で表すことのできる圏です。以下の図を見てください。
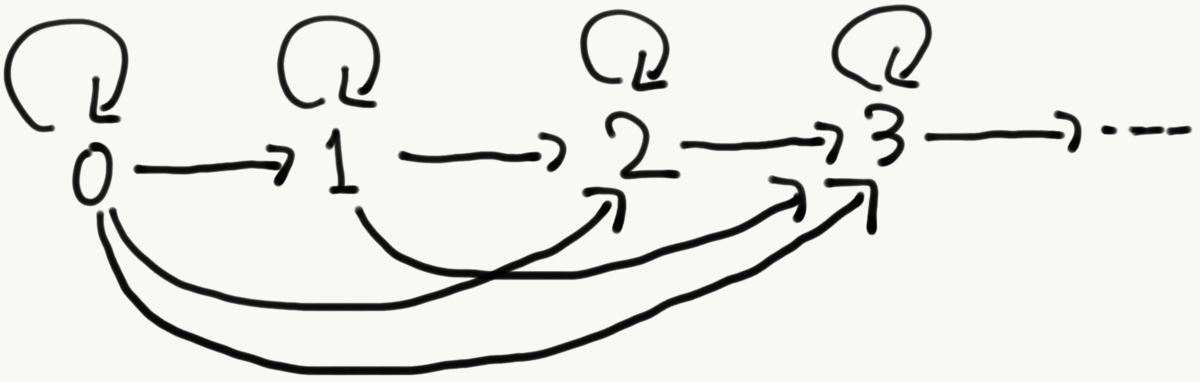
この図には、対象が存在し、それぞれの射が前順序を表しています。
図中の射が表す前順序を書き下すと、次のようになります。
恒等射:
恒等射以外の射:
おわりに
以上、まだまだ修正点はあるかもしれませんが、圏論の初歩の内容のまとめを、おふとんアイコンのT先輩の力を借りながらやってみました。 ご覧いただき、ありがとうございました。
今後、Catsや圏論をしっかり理解して、関数型プログラミング言語をより高度に使いこなして、より良い広告配信システムを作っていきたいと思います。
マイクロアドでは 「広告配信システムをつくりたい!」 「関数型プログラミング言語をガンガン使っていきたい!」 「圏論を理解できるようになりたい!」 「おふとんアイコンの先輩にレビューしてもらいたい!」 というエンジニアを積極的に募集しています。 ご興味を持たれた方はこちらから是非ご応募下さい!
※チャットのやり取りは一部フィクションです



