こんにちは、機械学習エンジニアの岸本です。マイクロアドのシステムにおいて、機械学習などデータ解析が関わる部分の研究開発を行っています。

学生時代は、医用画像を対象とした医師の診断を支援するシステム (Computer-Aided Diagnosis; CAD) の研究開発を行っていました。マイクロアドに入社してからは、画像解析や広告配信のログを対象とした機械学習を行ってきましたが、最近では主に自然言語処理を行っています。

広告配信をユーザへの広告のレコメンドと捉えると、ユーザに対してWebページの閲覧履歴などから、「何にどれだけ興味があるか」を定量的に評価することが重要です。そこでWebページに記載されている内容から、トピックを推定したり重要なキーワードを抽出したりすることが必要になってきます。マイクロアドでは、こういったところで自然言語処理を活用しています。

自然言語処理においてWikipediaのデータは非常に重要です。最も大きな用途でいえば、大規模なテキストコーパスとして利用されています。またテキストの情報以外にも、記事同士のリンクなど活用できそうな情報が多く含まれています。

今回は、Studio Ousiaがオープンソースとして公開したWikipedia2Vecと、その文書分類タスクへの応用結果を紹介したいと思います。

Wikipedia2Vecとは
文書分類タスクへの応用
- 方法
- 結果
まとめ

Wikipedia2Vecとは

Wikipedia2Vec *1 はWord2Vec *2 の拡張であり、Wikipediaの単語とエンティティを同一なベクトル空間に写像する分散表現 *3 を学習します。ここでエンティティとは、Wikipediaで一意のURLを持つエントリ、つまりWikipediaの記事のタイトルを指します。学習した分散表現を用いて、単語間・エンティティ間・単語とエンティティ間の類似度を評価したり、文書分類タスクに応用したりすることが可能です。まず、ベースであるWord2Vecについて軽く説明したいと思います。

Word2Vec

Word2Vecは、分散表現を獲得したい単語（ターゲット）とその周囲の単語（コンテキスト）を用いて、分散表現を学習します。Word2Vecでは具体的にはニューラルネットワークを用いてモデルを学習しますが、問題設定による違いで、Continuous Bag-of-Words (CBOW) モデルとskip-gramモデルという2つのモデルが存在します。CBOWでは、コンテキストが与えられたときターゲットを予測し、skip-gramではターゲットからコンテキストを予測します。よく使用される、skip-gramモデルについて説明します。

skip-gramモデル

前述したようにニューラルネットワークによりモデルを構築しますが、そのために単語を以下のようなone-hot表現に変換します。ここでのone-hot表現は、ベクトル中の対応する単語のインデックスのみ1で、残りは全て0であるようなベクトル表現です。

skip-gramではターゲットからコンテキストを予測するので、one-hot表現を用いて以下のようなネットワーク構造を考えます。これはターゲットが important で、コンテキストが more と than の場合です。入力層がターゲットの単語、出力層がコンテキストの単語を表現し、入力のターゲットからコンテキストを予測できるように学習を行います。つまり、ターゲットの単語のone-hot表現が入力、コンテキストの各単語のone-hot表現が教師信号です。以下の図において、点線で囲まれている部分は全結合を表します。

上図において、中間層のユニット数を3としているので、 $\mathrm{W}_{in}$ は $(6 \times 3)$ となります。

この、 $\mathrm{W}_{in}$ の各行が対応する各単語の分散表現となります。*4

次にWikipedia2Vecを紹介するにあたり、skip-gramの数式による表現を導入したいと思います。表記の簡単さのため、 $\mathrm{W}_{in}$ を $\mathrm{V}$ 、 $\mathrm{W}_{out}$ を $\mathrm{U}$ とします。skip-gramでは、単語の数列 $w_1, w_2, ..., w_T$ が与えられたとき次の目的関数を最大化することを目標とします。

$$ \mathcal{L}_w = \sum^{T}_{t=1} \sum_{-c \leq j \leq c, j \neq 0} \log P(w_{t+j} | w_t) $$

ここで $c$ はコンテキストのウィンドウサイズ（ターゲットの左右何単語をコンテキストとして含めるか）、 $w_t$ はターゲット、 $w_{t+j}$ はコンテキストです。条件付き確率 $P(w_{t+j} | w_t)$ は以下のソフトマックス関数で計算されます。

$$ P(w_{t+j} | w_t) = \frac{\exp(\mathrm{V}_{w_t}^{T} \mathrm{U}_{w_{t+j}})}{\sum_{w \in W} \exp (\mathrm{V}_{w_t}^{T} \mathrm{U}_{w}) } $$

ここで $W$ は全ての単語の集合、 $\mathrm{V}_{w} \in \mathbb{R}^{d}$ と $\mathrm{U}_{w} \in \mathbb{R}^{d}$ はそれぞれ行列 $\mathrm{V}$ と $\mathrm{U}$ における単語 $w$ に対応するベクトルです。

繰り返しにはなりますが、skip-gramでは、目的関数 $\mathcal{L}_w$ を最大化するように学習を行い、行列 $\mathrm{V}$ の行ベクトルが各単語の分散表現となります。

Wikipedia2Vec

先に説明したように、Wikipedia2VecはWord2Vec（具体的にはskip-gram）を拡張して、Wikipediaの単語とエンティティを同一なベクトル空間に写像する分散表現を学習する仕組みです。skip-gram に KB graph model と anchor context model というモデルを追加します。ここで、KBはknowledge baseの略であり、Wikipedia2VecにおけるKBの実態はWikipediaです。

以下の画像はWikipedia2Vecの開発者の講演資料から引用したKB graph modelとanchor context modelの概念図です。左図はKB graph modelの概念図であり、エンティティが与えられたとき、そのエンティティにリンクしている他のエンティティを予測する問題を考えます。右図はanchor context modelの概念図であり、エンティティが与えられたとき、そのエンティティを指しているリンクの周辺の単語を予測する問題を考えます。

f:id:pompom168:20181113114121p:plain — https://github.com/ikuyamada/wikipedia-nlp/blob/master/resources/pydata_slides.pdf より引用

skip-gramとの対比で考えると、KB graph modelはskip-gramにおける単語がエンティティに置き換わったイメージで、anchor context modelはskip-gramにおけるターゲットがエンティティを指している本文中のリンクのみであるイメージでしょうか。また、KB graph modelだけでなくanchor context modelまで考えるのは、KB graph modelを加えただけでは単語とエンティティがベクトル空間中の異なる部分空間に写像されてしまうからです。

次に、KB graph modelとanchor context modelの目的関数を紹介します。

KB graph modelでは、以下のように目的関数が定式化されます。

$$ \mathcal{L}_e = \sum_{e_i \in E} \sum_{e_o \in C_{e_i}, e_i \neq e_o} \log P(e_o | e_i) $$

ここで $e_i$ はターゲットのエンティティ、 $e_o$ は $e_i$ にリンクしているエンティティ、 $E$ はWikipediaにおける全エンティティの集合、 $C_{e_i}$ は $e_i$ にリンクしている全エンティティの集合です。条件付き確率 $P(e_o | e_i)$ は以下のソフトマックス関数で計算されます。

$$ P(e_o | e_i) = \frac{\exp(\mathrm{V}_{e_i}^{T} \mathrm{U}_{e_{o}})}{\sum_{e \in E} \exp (\mathrm{V}_{e_i}^{T} \mathrm{U}_{e}) } $$

anchor context modelでは、以下のように目的関数が定式化されます。

$$ \mathcal{L}_a = \sum_{(e_i, Q) \in A} \sum_{w_o \in Q} \log P(w_o | e_i) $$

ここで $A$ はWikipediaにおけるエンティティが指しているリンクの集合、エンティティ $e_i$ とそのコンテキスト $Q$ は集合 $A$ の要素です。条件付き確率 $P(w_o | e_i)$ は以下のソフトマックス関数で計算されます。

$$ P(w_o | e_i) = \frac{\exp(\mathrm{V}_{e_i}^{T} \mathrm{U}_{w_{o}})}{\sum_{w \in W} \exp (\mathrm{V}_{e_i}^{T} \mathrm{U}_{w}) } $$

Wikipedia2Vecでは、以上のskip-gram、KB graph model、anchor context modelの目的関数を足し合わせて目的関数を定義し、最大化するように学習を行います。

$$ \mathcal{L} = \mathcal{L}_w + \mathcal{L}_e + \mathcal{L}_a $$

使用例

Wikipedia2VecはPyPIに登録されており、pipでインストールできます。

pip install wikipedia2vec

また、今回は学習済のモデルを使用したいと思います。こちらから日本語のコーパスで100次元の分散表現を学習したモデルをダウンロードします。それではUsageに従って一通り触ってみたいと思います。

以下の例の中で、 くまもん からエンティティである くまモン を抽出できています。これがWikipedia2Vecのライブラリで実装されているもう1つの便利な機能です。表記揺れにもある程度対応できそうです。くまもん から抽出されたエンティティ くまモン と類似度が高いものとして ロアッソくん などゆるキャラと思われるものが選ばれています。またエンティティだけでなく、単語である バリィ （おそらくバリィさんでしょうか）も選ばれているところが、単語とエンティティを同じベクトル空間に写像できるWikipedia2Vecの特徴です。また、get_entity_vectorメソッドを利用してエンティティの分散表現を獲得できます。

In [1]: from wikipedia2vec import Wikipedia2Vec                                 

In [2]: MODEL_FILE = 'jawiki_20180420_100d.pkl'                                 

In [3]: wiki2vec = Wikipedia2Vec.load(MODEL_FILE)                               

# エンティティを抽出
In [4]: wiki2vec.get_entity('くまもん')                                         
Out[4]: <Entity くまモン>

# エンティティと単語の中で類似度高い上位5個
In [5]: wiki2vec.most_similar(wiki2vec.get_entity('くまもん'), 5)               
Out[5]: 
[(<Entity くまモン>, 1.0000001),
 (<Entity ロアッソくん>, 0.66104835),
 (<Entity 火の国まつり>, 0.66021234),
 (<Entity やつしろ全国花火競技大会>, 0.65534824),
 (<Word バリィ>, 0.65516865)]

# 分散表現
In [6]: wiki2vec.get_entity_vector(wiki2vec.get_entity('くまもん').title)       
Out[6]: 
memmap([ 0.4987742 ,  0.4818462 , -0.31397748, -0.4299439 , -0.66615874,
        -1.1467521 , -0.64756006, -0.04232506, -0.01365009,  0.3819751 ,
        -0.81580204,  0.57949615,  0.3895943 , -0.02147516,  0.9058112 ,
        -0.32506028, -0.5522671 , -0.92519724, -1.008661  , -0.13105063,
         0.8929451 ,  0.00837045,  1.233129  ,  0.17471145,  0.3164325 ,
         0.6455574 ,  0.76717734,  0.93366736, -1.3345108 ,  0.68523425,
         0.16769607, -0.08323109, -0.29970533,  0.6999099 ,  0.8458802 ,
         0.07209787, -0.68666214, -0.96083575, -0.46374056,  0.6435073 ,
        -0.3621788 , -0.8010363 ,  0.7227319 ,  1.0075872 ,  1.043849  ,
        -0.48358604,  0.13965838, -0.7763062 , -0.6139373 , -0.12857266,
         0.84543735,  0.02338971,  1.4464204 ,  0.3906651 ,  0.59475774,
         0.6057169 , -0.15061677,  0.4464892 , -1.0475675 , -0.06334771,
         0.09552235,  0.16142467, -0.49505463,  0.616421  , -0.45328742,
         0.7267984 ,  0.2580754 ,  0.7739888 , -0.10459039,  1.0554446 ,
         0.14633359, -0.62125355,  0.20096089, -0.07766332,  0.66929936,
         0.81375283, -0.5216525 , -0.28748748,  1.1850187 ,  0.2794962 ,
         0.80120045, -0.41333124,  0.4394144 , -0.42725018,  0.20369242,
        -0.5351115 ,  1.212701  ,  0.25982308,  0.5155067 , -0.6502942 ,
         0.47976273,  0.6977755 , -0.9847092 , -0.90202516,  0.38431334,
        -0.01317564, -1.2650503 ,  0.24565668, -0.17786348,  0.05527222],
       dtype=float32)

文書分類タスクへの応用

Wikipedia2Vecの活用として、文書分類への応用をしてみたいと思います。実験に使用するデータセットとしてlivedoorニュースコーパス*5を利用します。livedoorニュースコーパスには以下の9個のカテゴリが存在するので、各文章を9個のクラスに分類する9クラス分類問題となります。

トピックニュース
Sports Watch
ITライフハック
家電チャンネル
MOVIE ENTER
独女通信
エスマックス
livedoor HOMME
Peachy

各カテゴリのサンプルサイズ（記事数）は以下の表のとおりです。

方法

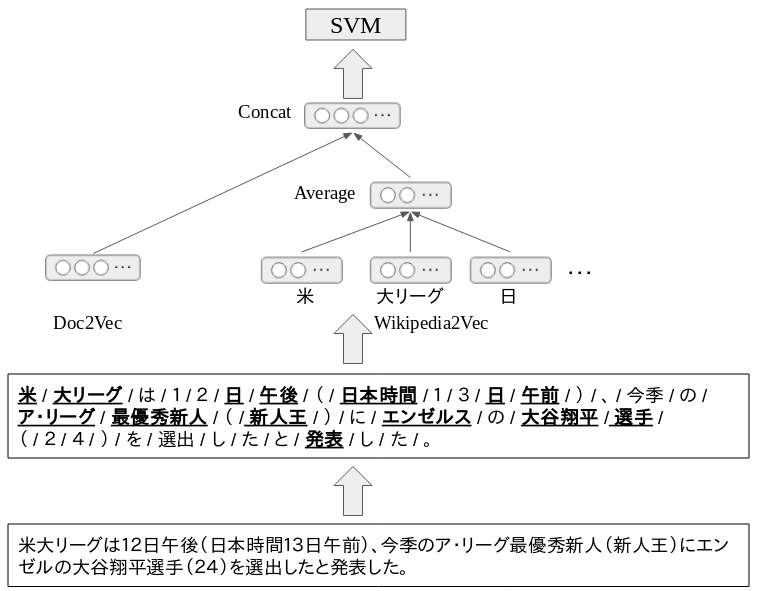
分類器全体のアーキテクチャは以下の図のようにしました。Studio OusiaがNIPSのコンペで優勝した際のアーキテクチャ*6を参考にして、少しアレンジを行いました。

文章が与えられると、まず分かち書きを行い単語に分割します。形態素解析エンジンにはMeCabを利用しました。次に、Doc2Vecに文章を入力し文章の分散表現を得ます。ここでDoc2vecは、Word2vecを拡張した文章の分散表現を学習する仕組みです。さらに分かち書きで得た単語の内、名詞のみを対象としエンティティを抽出して、Wikipedia2Vecによりエンティティの分散表現を得ます。エンティティの分散表現は1つの文章から抽出されたエンティティの数存在するので、これらの平均ベクトルを算出します。最後にDoc2Vecによる分散表現のベクトルと、Wikipedia2Vecによるエンティティの分散表現の平均ベクトルを連結し、これを入力としてSVMの学習・評価を行います。

Doc2Vec自体の学習にはlivedoorニュースコーパスを用い、Wikipedia2vecは前述の学習済モデルを使用しました。 Doc2Vecはgenismの実装を利用して、ハイパーパラメータはデフォルトのものを使用しました。つまり、Doc2Vec自体のチューニングは行っていません。

また比較のため、Doc2VecだけのパターンとWikipedia2Vecだけのパターンでも学習・評価を行いました。

結果

SVMのハイパーパラメータについて、以下の範囲を2-foldのCross Validationでグリッドサーチを行いました。Cross Validationの際、各クラスのサンプルサイズが同じ割合になるようにサンプリングを行いましたが、そもそもクラス間でサンプルサイズが異なることは、今回は考慮しませんでした。評価指標には多クラスのAccuracyを用いました。

param_grid = [
    {'C':[0.1, 1, 10, 100], 'kernel':'linear'},
    {'C':[0.1, 1, 10, 100], 'gamma':[0.1, 1, 10, 100], 'kernel':'rbf'}
]

Doc2Vecのみ、Wikipedia2Vecのみ、Doc2Vec+Wikipedia2Vecの3つのパターンにおいて、最良のAccuracyは以下のようになりました。 Doc2Vec < Wikipedia2Vec < Doc2Vec + Wikipedia2Vecの順にAccuracyが高くなりました。

Doc2Vecのチューニングを行っていないのでフェアではないですが、Wikipedia2vecと組み合わせることでAccurcyが向上していることから、対象の分類問題のドメインのテキスト情報にWikipediaの情報を補助的に使用することで、分類性能を向上させることができる可能性があることが分かりました。